The Zilliqa Design Story Piece by Piece: Part 3 (Making Consensus Efficient)
Note: ➤ We’re on Slack and on Telegram! Join our community, ask us questions, and get updated on the latest (and hopefully the greatest!)

In our previous article, we discussed why Zilliqa needs a different consensus protocol and why a classical Nakamoto (aka PoW) style consensus protocol is not ideal.
The consensus protocol used in Zilliqa is called Practical Byzantine Fault Tolerance, in short pBFT. The protocol comes with several advantages from being computationally cheap, and hence incurring a small energy footprint to providing transaction finality that eliminates the need for confirmations.
However, classical pBFT as designed by Castro and Liskov in their original paper is communication-efficient only when the consensus group is small, say less than 50 nodes. Communication between the nodes quickly becomes a bottleneck when the consensus group becomes large, say around 600 nodes as we require in Zilliqa. Recall that any consensus group in Zilliqa must have at least 600 nodes to ensure (with high probability) that less than 1/3 of them are Byzantine.
In this last part of the series, we discuss how high the communication requirement of the classical pBFT protocol is and how we reduce it using a primitive called multi-signature.
In the rest of this article, we use n to denote the size of a consensus group. In the context of Zilliqa, n can be assumed to be 600.
Communication cost of pBFT
pBFT requires all honest nodes to agree on the state of the system and hence requires nodes to communicate heavily with each other. The protocol as described in the original paper requires each node to communicate with every other node to share protocol messages. This implies that each node has to send n messages. Hence, the total communication requirement is of the order of n².
Cost of authenticating messages
Furthermore, simply sending a message in a Byzantine network is not enough. In particular, when a node A receives a message from another node B in an open Byzantine network, A has to be sure that the message was indeed sent by B and that the message was not modified during the transmission. Without such guarantees, it becomes difficult for a node to ensure the authenticity of a message as a man-in-the-middle attacker can modify the message en route and give an incorrect view to the nodes.
A solution to authenticate message transmission is to generate a key that is kept secret between A and B. The key can then be used to generate a tag for every outgoing message. As the key is known only to A and B, the tag can only be generated by either A or B. The tag then allows them to authenticate the source of the message.
Message authentication code (MAC) is a cryptographic primitive that can generate such a tag. One possible way to construct a MAC is to use a cryptographic hash function that takes the key and a message as inputs and generates a tag as the output.
The figure below shows how a MAC can be used by a sender and a receiver. The sender computes the tag using the message and the secret key and sends it along with the message to the receiver. The receiver then recomputes the MAC and checks whether the resulting tag is the same as the one received. If the two tags are the same, then the message has not been altered.
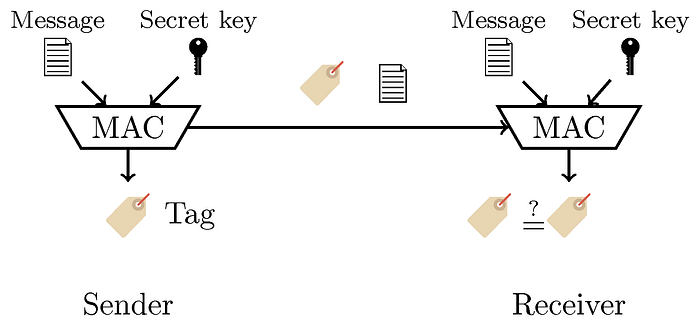
However, an issue with MAC and in general with most symmetric-key primitives is that if we have n nodes, one needs a secret key per pair of nodes. Hence, if we have n nodes, a total of n(n-1)/2 keys are required.
Let us now dig a little deeper and analyze the communication cost of using a MAC. Imagine we have 4 nodes in the network: A, B, C and D. A needs to send a message to the entire network, i.e, to B, C and D. So, A will have to create 3 different tags as A shares a different key with each B, C and D. Now, let us say A wishes to use B as a relay to transport his tags to C and D, then, A will need to send 3 tags to B (Cf. figure below). Similarly, when B needs to forward A’s tags to C and D, it may decide to use C as a relay. Since B has already received the tag meant for it, it will send only 2 tags to C and so on. The total number of messages shared using this simple relay-based broadcast mechanism will be 3+2+1 = 6.
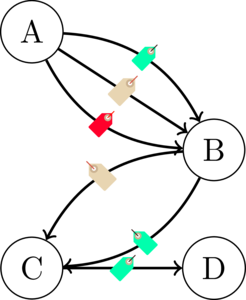
For a network with n nodes, if we use MAC, then the total number of messages (in the form of tags) communicated will be: (n-1) + (n-2) + … + 1 = n (n-1)/2.
Public key cryptography to improve efficiency
MAC can in fact be replaced by digital signatures as verifying a signature on a message also ensures that the message was indeed signed by a legitimate sender. The reason why Castro and Liskov did not use digital signatures was that computing MAC back then was much cheaper than producing a digital signature. Nowadays, digital signatures are pretty cheap.
Moreover, public-key cryptography comes with its own benefits. To see this, we continue with the previous example with four nodes A, B, C and D. We now assume that nodes use digital signatures. Hence, when A sends a message out, it will sign the message and produce a signature. The signature will then be sent to the next hop B as earlier. Note that A does not need to create 3 signatures here, only a single signature is enough. So, B only receives a single message and the corresponding signature. B will then forward the (message, signature) pair to the next hop C and so on. At each hop, a single signature is being forwarded. The total number of messages shared in this case will be 1+1+1 = 3.

For a network with n nodes, if we use digital signatures, then the total number of messages communicated will be: 1 + 1 + 1 … (n-1) times = n-1.
The idea of replacing MAC by digital signatures was recently proposed in an academic paper.
The use of digital signatures (instead of MAC) reduces the number of messages from quadratic to linear. This reduction has an important impact when n is large say 600, where, the number of messages communicated reduces from 179,700 to 599.
Reducing the size of each message using a multi-signature scheme
The story so far should convince you that it is better to use digital signatures than MAC to reduce the number of transmitted messages. So, what do we do now, …, well, let us do the obvious and replace MAC by digital signatures in the classical pBFT protocol.
Now, the question is, can we do better than digital signatures? The answer is yes, there is still some room for improvement. The meat of the blog is yet to come! But, let us first locate where exactly can we improve.
Recall that pBFT gives finality to transactions which means that once a transaction has been committed to a blockchain, it’s final and temporary forks do not occur, hence no need for confirmations. Finality comes from the fact that pBFT requires each block to be signed by a supermajority of honest nodes in the consensus group. By signing, each honest node affirms that it has verified the contents of the block and that the transactions are valid. In a PoW-based consensus, a node generates a block and the rest of the network either accepts it or rejects it, this leads to temporary forks.
Consider the following method of signing, each node signs a block and then forwards the signed block to the rest of the network, each node then appends its own signature and eventually after sufficient communication, the block gets a supermajority of signatures from each honest node. In the worst case, where every node (including the malicious ones) in the network signs the block, the signature part of the block will have a size of n. And this is where multi-signatures come in.
Multi-signatures are a cryptographic primitive to aggregate n signatures on a message from n parties into a signature of constant size.
How does a (simplified) multi-signature work?
Before jumping into the details, let us first explain the setup. In a multi-signature scheme, we have n signers each with a (public, private) key pair, a verifier to verify the final signature and an aggregator which plays the role of a facilitator and aggregates the “signatures” sent by each individual signer. Let us also assume for this simplified description that every node is kind of honest and will cooperate in signing the message.
When an aggregated signature is verified by a verifier, the latter checks whether all the signers have properly signed or not. Signature verification succeeds only when all the signers have properly signed. If any one of the signer misbehaves, then the signature verification fails.
We are now ready to delve into the details. Sit tight as it will get a little technical.
A multi-signature scheme basically runs in two steps. In the first step of the protocol, each node will send its public key to the aggregator. All the public keys are then aggregated to generate a single public key. Depending on the mathematical form of the keys, the aggregation could simply be a simple addition or a multiplication.
E.g., Aggregated Public key = Public key_1 + Public key_2 + …. + Public key_n.
The aggregated public key can then be forwarded to the verifier who can use it to verify an aggregated signature. The aggregator also sends the message to be signed to each of the signers.
In the second step, the aggregator initiates an interactive protocol with each of the signers. The interactive protocol runs in three phases:
- Commit phase: In the commit phase, each node generates some randomness and commits to it. For those who do not understand what a cryptographic commitment is, consider the following analogy: each node will secretly roll a dice, write down the outcome on a sheet of paper and put it in a box, lock it and send it to the aggregator. The aggregator should not be able to open the box.
- Challenge phase: In the challenge phase, the aggregator first aggregates each commitment again using addition or multiplication. It then generates a challenge using the aggregated commitment, the aggregated public key and the message. The challenge is then sent to each node. The challenge is later used to confirm that each node indeed knows the private key for the public key. This is similar to how regular digital signatures work, where a signature proves that the signer indeed knows the private key.
- Response phase: Each node then responds to the challenge by sending a response that requires the use of its private key. Responses are then aggregated by the aggregator. Each response is sort of a proof that the signer knows the private key for its public key.
The final aggregated signature is then the pair (challenge, aggregated response) which can be verified against the aggregated public key generated in the first step.
Note that the size of the aggregated signature is constant and does not depend on the number of signers.

When the verifier checks the aggregated signature, it does not check whether each signer has properly followed the protocol, it only checks whether all the signers have collectively followed the protocol and have proven the knowledge of their private keys. Hence, the verifier makes an all-or-nothing decision.
A popular multi-signature scheme is based on Schnorr digital signatures and was popularized by an academic paper that uses it in a setting where some witnesses need to attest the occurrence of an event.
Conclusion
Zilliqa uses several techniques developed in recent academic papers to improve the efficiency of the classical pBFT protocol.
The main highlight of this article is the multi-signature protocol that reduces the number of signatures from n to 1 and hence reduces the size of the agreed-upon block.
There are some questions that remain unanswered, the most crucial one being what happens when only a supermajority signs the message, but not all the nodes. Will the protocol still work? What sort of changes should one make to the protocol?
Also, can you think of an attack on the simplified version of the multi-signature protocol?
There are two ways you can get answers to these questions. The hard way is to read the Zilliqa technical whitepaper. The easy way is by asking the same questions back to us on our community channels. Pick your way and let us know.
➤ Ask us questions on Slack or Telegram or Gitter.
➤ Follow us on Twitter,
➤ Subscribe to our Newsletter,
➤ Subscribe to our Blog,
Icons used in this article are made by Freepik from www.flaticon.com
